Чтобы найти силу, действующую на вращающийся объект произвольной формы, центр масс которого движется в некоторой среде, воспользуемся теоремой Жуковского. Тогда будет верно следующее:

(4.1.1)

– сила, действующая на тело, ρ – плотность среды,

– скорость потока среды обтекающего тело, dl – элемент тела длины l.

(4.1.2)

– скорость элемента поверхности тела, dk – элемент внешнего контура k рассматриваемого тела.
Если тело вращается вокруг оси, по которой измеряется длина тела l, удобно записать интеграл

через угловую скорость

в полярных координатах:
 d\phi dk=2\vec{\omega}S)
(4.1.3)
S – площадь сечения рассматриваемого тела, ограниченного внешним контуром, на каждом элементе тела длины dl. Тогда проинтегрировав (4.1.3) по dl мы получим:

(4.1.4)
Где V – объём рассматриваемого тела. При этом (1) запишется в виде:

(4.1.5)
Эту формулу для удобства можно записать в нескольких вариантах. Т.к. скорость обтекающего потока будет обратной по отношению к скорости тела, движущегося в покоящейся среде, то

, а поскольку операция векторного умножения антикоммутативна, то:

(4.1.6.1)

(4.1.6.2)

(4.1.6.3)

(4.1.6.4)

– скорость тела,

– скорость среды,

– угловая скорость тела,

– плотность среды,

– объём тела,

– масса вытесненной телом среды.
Таким образом сила, действующая на произвольное вращающееся тело, движущееся в некоторой среде, может быть выражена всего через 3-4 параметра, которые легко определяются в инженерных задачах. Подробно можно рассмотреть на рисунке 4.1.1.
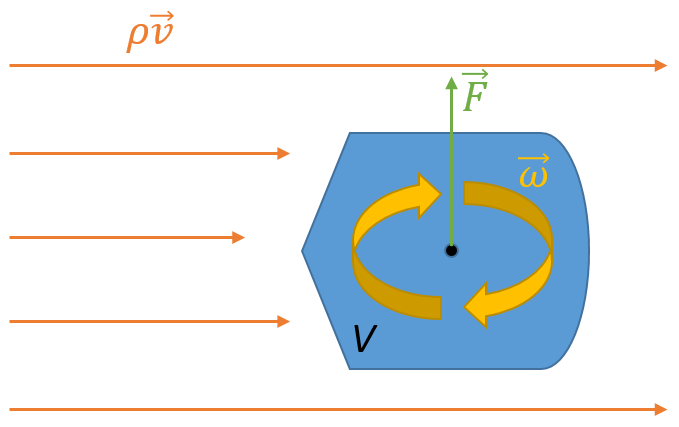
Рисунок 4.1.1. Силы, возникающие при обтекании вращающегося тела потоком газа или жидкости.
Обратим внимание, что сила направлена в сторону, где потоки сонаправлены, или, выражаясь точнее, разность скоростей меньше.
