В рамках современных представлений сила, действующая на заряд, движущийся в магнитном поле равна:

(4.6.1)
Или, если выразить заряд через его механическую модель:

(4.6.2)
В рамках же механических представлений та же сила будет равна:

(4.6.3)
Приравняем силы и сократим общие члены:

(4.6.4)
Из выражения 4.6.4 мы можем сделать вывод, что вектор магнитной индукции равен отношению проекции вектора угловой скорости на некоторое направление

, к модулю этой угловой скорости или косинус угла между

и

с точностью до некоторого постоянного коэффициента. А с точки зрения физики процесса, изложенного в 4.1., влиять на величину возникающей силы кроме скорости потока и тела, плотности среды и угловой скорости тела может только ориентация вращающегося тела относительно набегающего потока.
Чтобы понять физический смысл вектора

, нужно рассмотреть несколько опытов, в которых так или иначе проявляется магнитная индукция.
Опыт 1.
Возьмём 2 бруска из магнитомягкого материала, в одном из которых будет узкий жёлоб, проходящий по середине одной из граней. В этот жёлоб положим проводник. Плотно прижмём 2 бруска так, чтобы проводник был между ними и кратковременно подведём к нему сильный ток (Рисунок 4.6.1). Магнитный поток замкнётся по линиям магнитной индукции

. Даже после прекращения подачи тока бруски останутся сцепленными. Причём сила этой сцепки оказывается весьма значительной. Однако если их разомкнуть, практически не остаётся остаточной намагниченности.
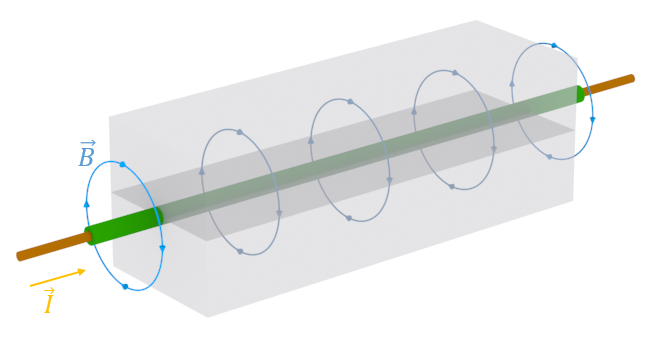
Рисунок 4.6.1. Опыт замыкания магнитного потока 1.
Опыт 2.
Сложим четыре бруска из магнитомягкого материала так, чтобы образовался квадрат. Вокруг одного из брусков поместим обмотку, к которой кратковременно подведём ток (Рисунок 4.6.2). Магнитный поток замкнётся через все четыре бруска. Даже после прекращения подачи тока бруски останутся сцепленными. Сила сцепки снова будет иметь высокое значение. Если убрать хотя бы один из брусков, сцепка пропадает. Остаточной намагниченности практически нет.
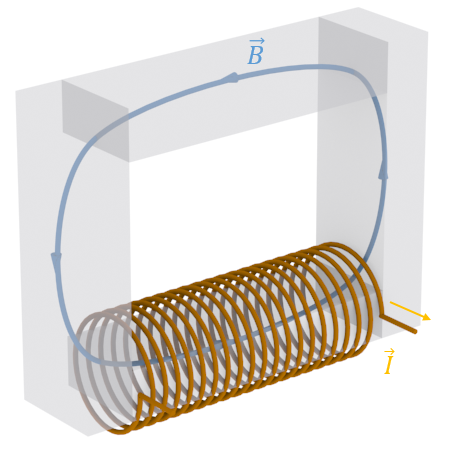
Рисунок 4.6.2. Опыт замыкания магнитного потока 2.
Опыт 3.
Возьмём 2 проводника, положим их параллельно. Подведём к ним ток в одном направлении. Проводники притягиваются. Магнитный поток замыкается вокруг них. Если же подвести ток в разных направлениях, проводники будут отталкиваться.
Сразу отметим, что из опыта 3 следует, что магнитная индукция – это не ламинарный поток эфира, т.к. в этом случае проводники вели бы себя наоборот. При однонаправленном токе отталкивались, а при разнонаправленном – притягивались. Кроме ламинарного потока на ориентацию частицы может влиять неравномерность потока, как говорится в главе 4.2.4.. Предлагается следующая модель для определения вектора магнитной индукции, применительно к силе Лоренца:
Вектор магнитной индукции равен косинусу угла между ротором скорости потока эфира и угловой скоростью заряженной частицы в направлении ротора скорости потока эфира с точностью до некоторого безразмерного коэффициента.
Действительно, в первом опыте поток эфира, создаваемый током, движущийся с ним в одном направлении будет убывать. Это убывание и породит ротор, который будет ориентировать, попавшие в поток заряженные частицы. Ориентированные заряженные частицы буду иметь единое направление кольцевого вращение, которое будет замыкаться вихрем по кругу вдоль направления потока магнитной индукции. Как только мы разорвём эту связь, вихрь распадётся. При повторном смыкании брусков заряженные частицы уже не имеют круговой ориентации, потому сцепления не произойдёт.
Во втором опыте внутри круговых витков ротор потока эфира и, соответственно, магнитная индукция будут куда более существенными. Именно это и следует из практики работы с катушками. На внешней стороне катушки ротор будет иметь меньшее значение и обратный знак. Снова заряженные частицы ориентируются вдоль потока магнитной индукции, образуя замкнутый вихрь. Имеем аналогичную первому опыту ситуацию.
В опыте с протеканием тока по параллельным проводникам процессы иные, однако порождены теми же явлениями. Рассмотрим рисунок 4.6.3.

Рисунок 4.6.3. Протекание тока в параллельных проводниках в одном направлении.
Представляя ток ламинарным потоком эфира, можем исходя из механических соображений предположить, что он увлекает за собой прилегающий к проводнику эфир. Затем построим зависимость затухания скорости этого потока с удалением от источника. Т.к. между проводниками эфир увлекается обоими проводами, его скорость

будет выше, чем скорость потока на внешней стороне

. Применив к этой системе закон Бернулли получим, что давление эфира между проводами окажется меньше, чем давление эфира вокруг проводов. Будут наблюдаться силы притяжения между проводниками.
Теперь рассмотрим обратную ситуацию, изображённую на рисунке 4.6.4.

Рисунок 4.6.4. Протекание тока в параллельных проводниках в разных направлениях.
Аналогично описанному выше скорости увлекаемого эфира

и

будут зависеть от силы тока и ориентации проводников. В данном случае

будет иметь фактически нулевое значение. Следовательно, по закону Бернулли статическое давление будет иметь максимальное значение. А

будет иметь некоторое существенное значение. Отсюда падение давления на внешней границе системы. Таким образом будет наблюдаться отталкивание проводников.
Итак, предложенная схема пригодна для объяснения силы Лоренца и силы Ампера. Удалось привести механическую модель образования сил, связанных с магнитной индукцией, дать ей механическую интерпретацию, непротиворечиво связанную со всеми изложенными ранее представлениями.



