Рассмотрим 2 заряженные частицы.
Аппроксимируем модель элементарной частицы вращающимся шаром.
Тогда его угловую скорость будем обозначать w, соответствующую скорость поверхности частицы – v, скорость обтекающего потока – u. Сила Магнуса, действующая на частицу будет обозначаться F. Это изображено на рисунке 4.4.1.
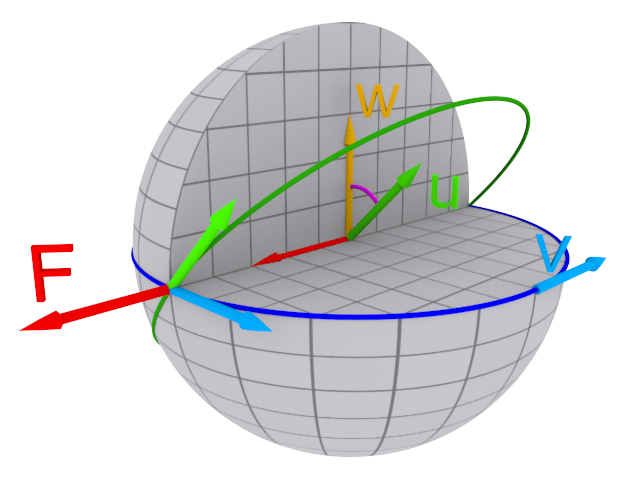
Рисунок 4.4.1. Аппроксимированная шаром модель элементарной частицы.
В рамках 4.3. показано, что любые 2 элементарные частицы (по крайней мере в невырожденных случаях) встанут параллельно. Тогда те частицы, у которых направление кольцевого вращения одинаково, будут взаимодействовать следующим образом: одна частица будет увлекать вместе с собственным кольцевым вращением эфир, создавая поток. Вторая частица будет находиться в этом потоке. Тогда такая постановка полностью описывается изложенным в главе 4.1. методом.
Сила, действующая на частицу будет рассчитываться по формуле 4.1.6.3. и равна

.
Чтобы определить все параметры, входящие в эту формулу, необходимо изучить экспериментальные и теоретические данные, известные в современной физике. Попробуем проанализировать одно из уравнений Максвелла:

(4.4.1)
При этом для неполяризуемой среды

(4.4.2)
По определению

– это сила, действующая на единичный заряд со стороны электрического поля,

– параметры, отвечающие за среду, в которой происходит взаимодействие. Источником этого поля является заряд Q. Исходя из представленной в главе 3 модели элементарной частицы, интенсивность кольцевого вращения эфира на поверхности частицы будет определяться из выражения ρvS, где ρ – это плотность эфира, v – скорость кольцевого вращения на поверхности частицы, S – эффективная площадь элементарной частицы, которая вовлекает во вращение окружающий частицу эфир. Именно это выражение и будет отвечать за заряд. Таким образом

(4.4.3)
Но и из уравнений Максвелла следует, что заряд равен интегральной сумме электрической индукции по некоторой поверхности, т.е. электрическая индукция как раз и будет соответствовать ρv. Поскольку за параметры среды в 4.4.2. отвечает только

, то именно это выражение и будет являться плотностью эфира. Т.е. мы получили принципиальный вывод о том, что диэлектрическая постоянная

является ничем иным, как плотностью эфира, и соответственно равна

кг/м^3. А величина Е по модулю будет соответствовать скорости эфира. Однако стоит отметить, что E направлена от заряда, а v будет ей перпендикулярна. Тогда для протона, пользуясь выражением 4.1.6.3. и выражением для определения угловой скорости

(

-радиус протона), можем записать следующее выражение для силы, действующей со стороны электрического поля на заряд:

(4.4.4)
Для двух элементарных зарядов на расстоянии 1 метр по законам электродинамики расчётное значение силы равно

Н. Скорость потока, сопоставляемого с электрическим полем, испускаемым одним зарядом будет равна

. Тогда на расстоянии метр, раскрыв векторное произведение, мы получим следующее выражение для силы:

(4.4.5)
Подставив известные значения для вакуума и протона, получим:

(4.4.6)
Тогда получим грубую оценку скорости вращения поверхности протона, равную

м/с.
Соответственно, если в одном теле таких зарядов много, то пропорционально возрастут объёмы и площади частиц. И силы будут пропорциональны количеству элементарных зарядов, как и в рамках традиционных взглядов электродинамики.
Теперь запишем выражение для силы Кулона:

(4.4.7)
Приняв

и

, где

и

– количество элементарных зарядов, участвующих во взаимодействии, в первом и втором теле, получим:

(4.4.8)
Выражение

отражает скорость потока, порождённого одним из заряженных тел в области пространства, где расположено второе тело.

– площадь поверхности зарядов второго тела, на которые производится взаимодействие.

– плотность среды, в которой происходит взаимодействие.

– скорость вращения второго зарядов второго тела. Таким образом мы получили полное соответствие выражения силы Кулона предложенной модели. При этом в полученной формуле нет никаких нефизичных коэффициентов.
Теперь обратим внимание на размерности величин. Подставим в 4.4.8 все размерности:

(4.4.9)
Оказывается, что предложенная модель заряда не противоречит физике и логике процесса. Отсюда мы можем сделать вывод о размерностях всех известных единиц измерения, участвующих в электромагнитных процессах к механике, т.е. выразить через килограмм, метр и секунду.
Теперь вспомним о векторе поляризации, который участвует в уравнениях Максвелла. Понятно, что представленная модель заряда элементарной частицы является величиной векторной

, где N – количество зарядов,

– площадь поверхности единичного заряда,

– радиус единичного заряда,

– угловая скорость заряда (оценочно равная

м/с). И если в силу изложенного в 4.3. любые 2 заряженных тела будут становиться параллельно и, соответственно взаимодействовать в полную силу, то в случае рассмотрения сложных систем, мы будем наблюдать отклонение от параллельного положения, которое и будет выражаться вектором поляризации

. Выходит, что вектор поляризации через традиционные величины электродинамики будет выражаться следующим выражением:
-1))
(4.4.10)
Где

– угол отклонения от параллельного положения зарядов.
Из вышеизложенного следует, что ε – это отношение плотности эфира в веществе к плотности эфира в вакууме.
Теперь обратим внимание, что значению электрической индукции в вакууме, равному 1 Кл/м^2 будет соответствовать скорость потока эфира, равная

м/с.
Итак, мы свели электростатическое взаимодействие к механике, получили значение плотности эфира, оценку скорости вращения поверхности протона и соответствующую угловую скорость, выяснили физический смысл электрической индукции и напряжённости и вектора поляризации.
