Гравитация, достоверно являясь отдельным фундаментальным взаимодействием, не может быть порождена теми же процессами, что и электромагнитное или ядерное взаимодействия. В главе 3 было высказано предположение, что эфир во внешнем сечении элементарной частицы будет охлаждаться (энергия хаотического движения частиц эфира будет меньше). Это будет порождать охлаждение и премыкающего к веществу эфира. Таким образом в ближней области вокруг любой вещественной материи эфир будет холоднее, чем вдали от вещества.
Из уравнений математической физики известно, что температура среды вокруг действующего источника тепла будет рассчитываться по формуле:
=q\frac{1}{4\pi k}\frac{1}{r}\frac{2}{\sqrt{\pi}}\int_{\frac{r}{2\sqrt{\alpha^2 t}}}^{\infty} e^{-\alpha^2} d\alpha)
(4.7.1)
Где r – расстояние от источника до рассматриваемой точки, t – время, q – мощность источника тепла, k – коэффициент теплопроводности, α – коэффициент температуропроводности.
При этом интеграл имеет следующий вид:
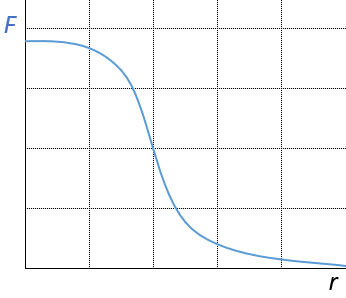
Рисунок 4.7.1. Значение интеграла в зависимости от радиус-вектора.
Видно, что для области, где r относительно невелико, интеграл принимает близкое к постоянному значение. А если все коэффициенты свернуть в один, то формулу 4.7.1 для области пространства, достаточно близкой к источнику тепла можно записать в следующем виде:
=Const\cdot\frac{q}{r})
(4.7.2)
Если процесс носит установившийся характер, то температура среды пропорциональна давлению. И можно записать аналогичное уравнение для давления, снова сворачивая все коэффициенты в единую константу:
=Const\cdot\frac{q}{r})
(4.7.3)
Таким образом любое тело, попавшее в рассматриваемую область пространства, будет испытывать на себе разность давлений, возникающую от разности температур. Эта разность давлений будет приложена к каждому нуклону, т.е. для любого нуклона, составляющего это тело будет верно:
=Const\cdot(\frac{q}{r}-\frac{q}{r%2B2r_p}))
(4.7.4)
Приведём к общему знаменателю:
=Const\cdot(\frac{q(r%2B2r_p)-qr}{r\cdot(r%2B2r_p)}))
(4.7.5)
Упростим и снова вынесем все постоянные в общий коэффициент:
=Const\cdot\frac{q}{r\cdot(r%2B2r_p)})
(4.7.6)
Если принять, что геометрические размеры тела много меньше расстояния между источником (или поглотителем) тепла и взаимодействующим телом, то для всех нуклонов можно считать r одинаковым, а

принять равным нулю:
=Const\cdot\frac{q}{r^2})
(4.7.7)
Суммарная разность давлений и сила будут пропорциональны количеству нуклонов и, соответственно, массе взаимодействующего тела. А мощность источника будет пропорциональна количеству его нуклонов и, соответственно, его массе. Тогда обозначим символом G результирующую константу. Тогда итоговое выражение возникающей силы примет вид:
=G\cdot\frac{m_1\cdot m_2}{r^2})
(4.7.8)
Полученная формула полностью соответствует современным представлениям о гравитации.
Если мы обратим внимание на наблюдения за небесными телами, то придём к выводу, что Меркурий и дальние планеты ведут себя не в полном соответствии с законом всемирного тяготения. Это объяснимо, т.к. принятые при выводе формулы допущения влияют именно на самую ближнюю и самую дальнюю области пространства.
Теперь вспомним, что указанное выражение для больших расстояний необходимо домножить на некоторый интеграл, вид которого изображён на рисунке 4.7.1. Из этого следует, что на дальних расстояниях сила гравитационного взаимодействия падает практически до нуля.
Если считать убывание силы гравитации пропорциональным квадрату расстояния и, что масса распределена по бесконечной вселенной относительно равномерно, возникает известный парадокс Неймана-Зелигера, в рамках которого оказывается, что в любой точке пространства гравитационный потенциал имеет бесконечное значение, а возникающие силы будут неопределёнными. Однако этот парадокс снимается в рамках предложенной модели при использовании интеграла 4.7.1.
Итак, мы аналитически вывели закон всемирного тяготения из модельных представлений, изложенных в главе 3, и избавились от известных противоречий в рамках теории гравитации.
